自由度 <<
Previous Next >> P_onshape
AI_plotter
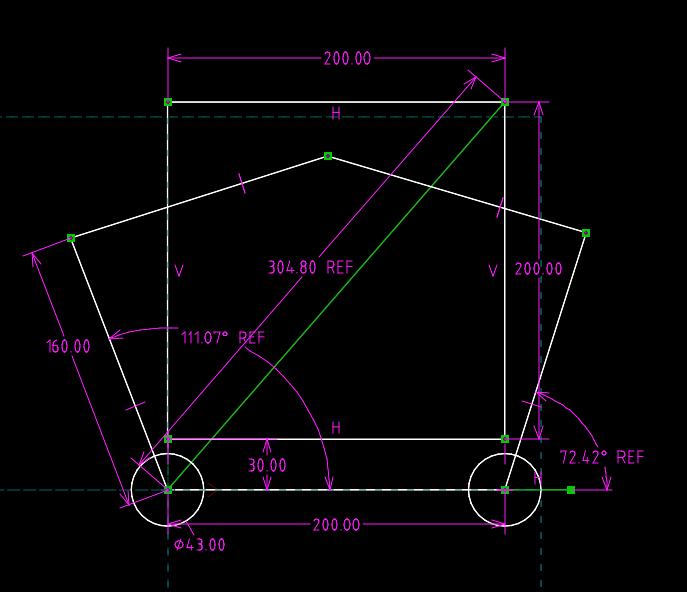
已知一個平面五連桿繪圖機購得兩個馬達的中心座標位於 (0,0), (200,0), 四根連桿長度皆為 160mm, 若 plotter 繪圖的座標點為 (x,y), (0,0) 位置上的馬達其轉角從正向 X 軸起算, 以逆時針方向為正, 其轉動角度為 t1, 而(200,0) 位置上的馬達其轉角也是從正向 X 軸起算, 也是以逆時針方向為正, 其轉動角度為 t2, 請利用 Python sympy 推導出以 x, y 為輸入變數, 求四組 t1 與 t2 作為輸出的逆向運動方程式。
plotter_sympy_inverse_kinematics.py
Plotter in Onshape

link1 tip center: -24.436, 158.123, 9 (模型放大兩倍,並轉為 m (-0.048872, 0.316246))
pen center: 96.762, 262.578, -3 (模型放大兩倍,並轉為 m,(0.193524, 0.525156))
link3 tip center: 218.635, 158.911, 15 (模型放大兩倍,並轉為 m,(0.43727, 0.317822))
right motor center: 200, 0, 15 (模型放大兩倍,並轉為 m,(0.4, 0))
left motor center: 0,0,0
Webots 場景檔案:
plotter_onshape_w3.7z (僅轉入馬達基座與左側 link1)
plotter_onshape_w4.7z (僅轉入馬達基座、左側link1 與 link2)
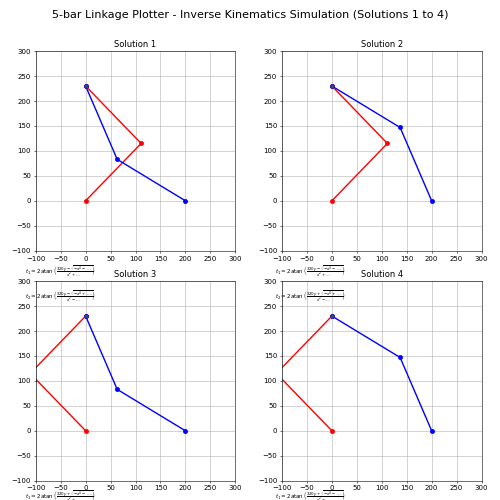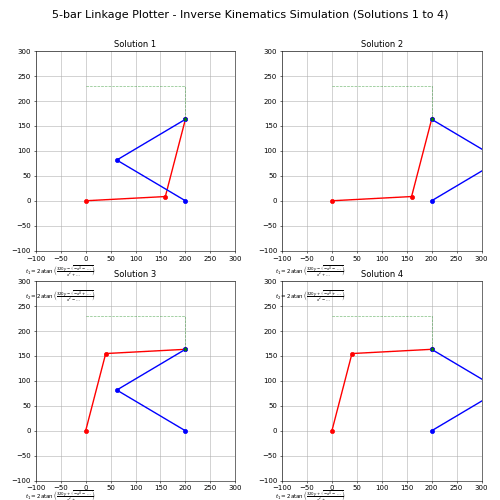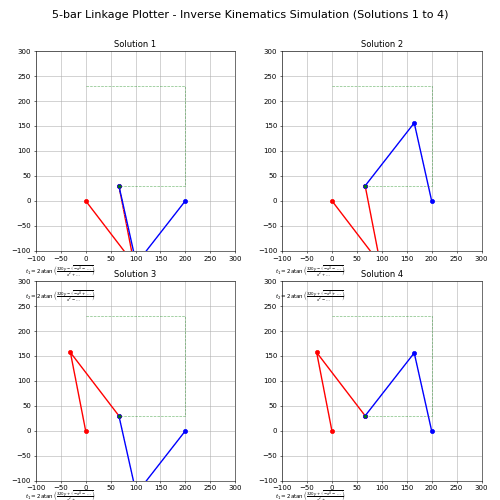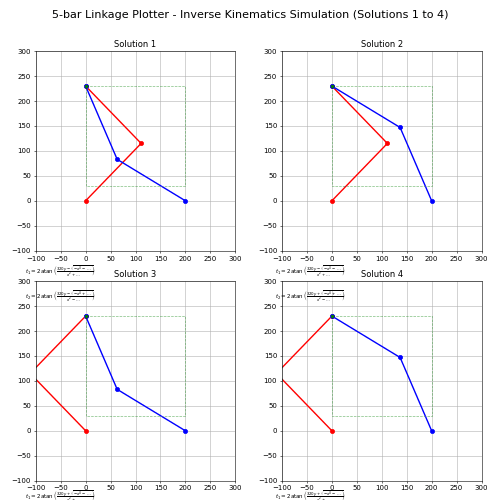
採 matplotlib 模擬四種掃掠 20cmx20cm 正方形邊長的逆向運動學 Solutions:
cad_demo_sym_formulation.py
cad_demo_check_sym_sol.py
Python math 格式:
def t1_sol1(x, y): return 2 * cmath.atan((320*y - cmath.sqrt(-x**4 - 2*x**2*y**2 + 102400*x**2 - y**4 + 102400*y**2)) / (x**2 + 320*x + y**2))
def t2_sol1(x, y): return 2 * cmath.atan((320*y + cmath.sqrt(-x**4 + 800*x**3 - 2*x**2*y**2 - 137600*x**2 + 800*x*y**2 - 8960000*x - y**4 + 22400*y**2 + 2496000000)) / (x**2 - 720*x + y**2 + 104000))
# Solution 2:
def t1_sol2(x, y): return 2 * cmath.atan((320*y - cmath.sqrt(-x**4 - 2*x**2*y**2 + 102400*x**2 - y**4 + 102400*y**2)) / (x**2 + 320*x + y**2))
def t2_sol2(x, y): return 2 * cmath.atan((320*y - cmath.sqrt(-x**4 + 800*x**3 - 2*x**2*y**2 - 137600*x**2 + 800*x*y**2 - 8960000*x - y**4 + 22400*y**2 + 2496000000)) / (x**2 - 720*x + y**2 + 104000))
# Solution 3:
def t1_sol3(x, y): return 2 * cmath.atan((320*y + cmath.sqrt(-x**4 - 2*x**2*y**2 + 102400*x**2 - y**4 + 102400*y**2)) / (x**2 + 320*x + y**2))
def t2_sol3(x, y): return 2 * cmath.atan((320*y + cmath.sqrt(-x**4 + 800*x**3 - 2*x**2*y**2 - 137600*x**2 + 800*x*y**2 - 8960000*x - y**4 + 22400*y**2 + 2496000000)) / (x**2 - 720*x + y**2 + 104000))
# Solution 4:
def t1_sol4(x, y): return 2 * cmath.atan((320*y + cmath.sqrt(-x**4 - 2*x**2*y**2 + 102400*x**2 - y**4 + 102400*y**2)) / (x**2 + 320*x + y**2))
def t2_sol4(x, y): return 2 * cmath.atan((320*y - cmath.sqrt(-x**4 + 800*x**3 - 2*x**2*y**2 - 137600*x**2 + 800*x*y**2 - 8960000*x - y**4 + 22400*y**2 + 2496000000)) / (x**2 - 720*x + y**2 + 104000))
mathjax 格式:
JSolution 1 (同上列 math 格式 Solution 2):
\[
t_{1} = 2 \operatorname{atan}{\left(\frac{320 y - \sqrt{- x^{4} - 2 x^{2} y^{2} + 102400 x^{2} - y^{4} + 102400 y^{2}}}{x^{2} + 320 x + y^{2}} \right)}
\]
\[
t_{2} = 2 \operatorname{atan}{\left(\frac{320 y - \sqrt{- x^{4} + 800 x^{3} - 2 x^{2} y^{2} - 137600 x^{2} + 800 x y^{2} - 8960000 x - y^{4} + 22400 y^{2} + 2496000000}}{x^{2} - 720 x + y^{2} + 104000} \right)}
\]
JSolution 2 (同上列 math 格式 Solution 1):
\[
t_{1} = 2 \operatorname{atan}{\left(\frac{320 y - \sqrt{- x^{4} - 2 x^{2} y^{2} + 102400 x^{2} - y^{4} + 102400 y^{2}}}{x^{2} + 320 x + y^{2}} \right)}
\]
\[
t_{2} = 2 \operatorname{atan}{\left(\frac{320 y + \sqrt{- x^{4} + 800 x^{3} - 2 x^{2} y^{2} - 137600 x^{2} + 800 x y^{2} - 8960000 x - y^{4} + 22400 y^{2} + 2496000000}}{x^{2} - 720 x + y^{2} + 104000} \right)}
\]
JSolution 3 (同上列 math 格式 Solution 4):
\[
t_{1} = 2 \operatorname{atan}{\left(\frac{320 y + \sqrt{- x^{4} - 2 x^{2} y^{2} + 102400 x^{2} - y^{4} + 102400 y^{2}}}{x^{2} + 320 x + y^{2}} \right)}
\]
\[
t_{2} = 2 \operatorname{atan}{\left(\frac{320 y - \sqrt{- x^{4} + 800 x^{3} - 2 x^{2} y^{2} - 137600 x^{2} + 800 x y^{2} - 8960000 x - y^{4} + 22400 y^{2} + 2496000000}}{x^{2} - 720 x + y^{2} + 104000} \right)}
\]
JSolution 4 (同上列 math 格式 Solution 3)::
\[
t_{1} = 2 \operatorname{atan}{\left(\frac{320 y + \sqrt{- x^{4} - 2 x^{2} y^{2} + 102400 x^{2} - y^{4} + 102400 y^{2}}}{x^{2} + 320 x + y^{2}} \right)}
\]
\[
t_{2} = 2 \operatorname{atan}{\left(\frac{320 y + \sqrt{- x^{4} + 800 x^{3} - 2 x^{2} y^{2} - 137600 x^{2} + 800 x y^{2} - 8960000 x - y^{4} + 22400 y^{2} + 2496000000}}{x^{2} - 720 x + y^{2} + 104000} \right)}
\]
上列符號式求解(Symbolic Formulation)與圖形法求解進行比較:
Plotter 到達點 (200, 230) 時的 t1 與 t2 角度(degree):
JSolution 3 (同上列 math 格式 Solution 4):
t1 = 66.72°
t2 = 45.95°
自由度 <<
Previous Next >> P_onshape