Homework << Previous Next >> Plotter

HW2

一個五連桿平面機構，固定點 A 與 E 的座標分別為 (0, 0), (-50, 0), link1 從 A 點連接向 B 點長度, 為一個直角三角形的斜邊, 此三角形的長邊尺寸為 50, 短邊尺寸為 45, link2 從 B 點連接向 C 點, 長度為 110, link3 從 C 點連接向 D 點長度也是 110, 而最後 link4 從 D 點連接向 E 點長度也是一個直角三角形的斜邊, 此三角形的長邊尺寸為 50, 短邊尺寸為 45。請問 link1 及 llink4 的長度分別為多少?

假設 A 點與 E 點分別裝設步進馬達, 其 A 點的旋轉角度是由其點右邊延伸水平線作為旋轉 0 度點，B 點起始點位於 X 軸上, 且旋轉方向為順時針方向, 而 E 點的旋轉角度則是由其點左邊延伸水平線作為旋轉 0 度點, D 點起始點也是位於 X 軸上, 且旋轉方向為逆時針方向旋轉, link1 的旋轉角度設為 theta1, 角度單位為 degree, 而 link4 的旋轉角度設為 theta2, 角度單位也是 degree, 請先利用此平面機構的兩個輸入角度作為函式的輸入變數, 用 link1 、link2、link3、link4 代表這四個連桿長度的符號名稱，且將此函數命名為 forward(theta1, theta2), 請利用正向運動學 (Forward Kinematics) 的方式，採符號運算法 (Symbolic Formulation)，利用 Python 的 sympy 模組, 讓 forward 函式的輸出為點 C 的 X 與 Y 座標。請推導。另外也請利用逆向運動學 (Inverse Kinematics) 的方式, 採符號運算法 (Symbolic Formulation)，利用 Python 的 sympy 模組, 讓 Inverse(C 點的 X 座標, C 點的 Y 座標) 函式的輸出為對應的 theta1 與 theta2 的轉角表示式。請推導, 且各推導過程均列出機構各點的 floating point 座標點的位置.

fivebar_robot_2d.slvs

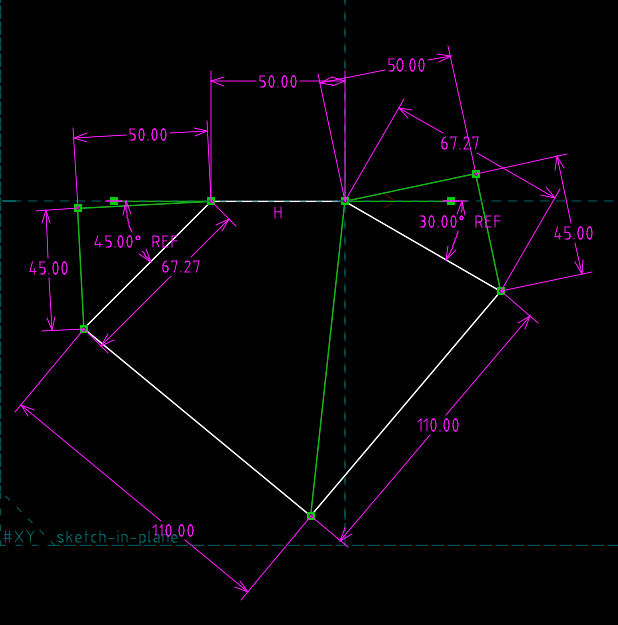
利用畢氏定理計算 link1 與 link4 的長度：

\[\sqrt{50^2 + 45^2} = \sqrt{2500 + 2025} = \sqrt{4525} \approx 67.27\]

因此定義如下:

import sympy as sp

L1 = L4 = sp.sqrt(45**2 + 50**2)  # ≈ 67.24
L2 = 110
L3 = 110

Forward Kinematics

目標是定義 forward(theta1, theta2) 輸出點 C 的 (x, y)。

幾何分析

點 A 為原點 (0, 0)，link1 由 A 旋轉 \(\theta_1\) 延伸至點 B。
點 E 座標為 (-50, 0)，link4 由 E 旋轉 \(\theta_2\) 延伸至點 D。
B 與 D 透過兩段連桿（link2 與 link3）連接，經過點 C。

先定義這些變數並推導 B、D、C 的位置。

forward 函式: fivebar_forward.py

import sympy as sp

# 正向運動學：給定角度與長度，求 C 點（兩個構型）
def forward(theta1_deg, theta2_deg, l1, l2, l3, l4):
    # 角度轉弧度，考慮旋轉方向
    theta1 = -theta1_deg * sp.pi / 180             # A 點，順時針
    theta2 = (180 + theta2_deg) * sp.pi / 180      # E 點，左水平方向起點，逆時針旋轉

    # 固定點座標
    Ax, Ay = 0, 0
    Ex, Ey = -50, 0

    # B, D 點位置
    Bx = Ax + l1 * sp.cos(theta1)
    By = Ay + l1 * sp.sin(theta1)
    Dx = Ex + l4 * sp.cos(theta2)
    Dy = Ey + l4 * sp.sin(theta2)

    # 向量 BD
    vec_x = Dx - Bx
    vec_y = Dy - By
    d = sp.sqrt(vec_x**2 + vec_y**2)

    # 中點 M
    Mx = (Bx + Dx) / 2
    My = (By + Dy) / 2

    # 高（從 M 垂直方向偏移）
    try:
        h = sp.sqrt(l2**2 - (d / 2)**2)
    except:
        raise ValueError("構型不可行：連桿無法形成三角形")

    # 單位向量 u = BD / ||BD||
    ux = vec_x / d
    uy = vec_y / d

    # 垂直向量（旋轉 90°）
    vx = -uy
    vy = ux

    # C 點 1（上構型）
    C1x = Mx + h * vx
    C1y = My + h * vy

    # C 點 2（下構型）
    C2x = Mx - h * vx
    C2y = My - h * vy

    print("B 點座標:", float(Bx.evalf()), float(By.evalf()))
    print("D 點座標:", float(Dx.evalf()), float(Dy.evalf()))
    print("C 點 1（上構型）:", float(C1x.evalf()), float(C1y.evalf()))
    print("C 點 2（下構型）:", float(C2x.evalf()), float(C2y.evalf()))

    return (float(C1x.evalf()), float(C1y.evalf())), (float(C2x.evalf()), float(C2y.evalf()))
    
print(forward(30, 45, 67.27, 110, 110, 67.27))

Inverse Kinematics: fivebar_inverse.py

現在要從點 C 的座標反推出 \(\theta_1, \theta_2\)。這部分相當複雜，因為存在多組解，因此我們專注於符號推導步驟。

幾何觀念

給定 C 點座標，要反推出：
B 點在以 A 為中心，半徑為 L1 的圓周上
D 點在以 E 為中心，半徑為 L4 的圓周上
B → C 與 D → C 分別長 L2, L3
使用向量反推、餘弦定理與 atan2 組合來求解旋轉角。

Inverse Kinematics:

# 逆向運動學：輸入 C 點位置與桿長，反推所有可能的角度組合
import sympy as sp

def inverse(cx_val, cy_val, l1_val, l2_val, l3_val, l4_val):
    # 定義符號變數
    Cx, Cy, L1, L2, L3, L4 = sp.symbols('Cx Cy L1 L2 L3 L4', real=True)

    # 固定點 A 與 E
    Ax, Ay = 0, 0
    Ex, Ey = -50, 0

    # ========== θ₁（順時針，從 +X 起算） ==========
    vec_A = sp.Matrix([Cx - Ax, Cy - Ay])
    r1 = vec_A.norm()
    angle_A = sp.atan2(vec_A[1], vec_A[0])
    cos_alpha1 = (L1**2 + r1**2 - L2**2) / (2 * L1 * r1)
    cos_alpha1 = sp.Max(-1, sp.Min(1, cos_alpha1))  # 保護 acos 領域
    alpha1 = sp.acos(cos_alpha1)
    theta1_a = -sp.deg(angle_A - alpha1)
    theta1_b = -sp.deg(angle_A + alpha1)

    # ========== θ₂（逆時針，從 –X 起算） ==========
    vec_E = sp.Matrix([Cx - Ex, Cy - Ey])
    r2 = vec_E.norm()
    angle_E = sp.atan2(vec_E[1], vec_E[0])
    cos_alpha2 = (L4**2 + r2**2 - L3**2) / (2 * L4 * r2)
    cos_alpha2 = sp.Max(-1, sp.Min(1, cos_alpha2))  # 保護 acos 領域
    alpha2 = sp.acos(cos_alpha2)
    # 補回 forward 中的 +180°
    theta2_a = sp.deg(angle_E - alpha2) - 180
    theta2_b = sp.deg(angle_E + alpha2) - 180

    # 數值代入
    subs = {
        Cx: cx_val,
        Cy: cy_val,
        L1: l1_val,
        L2: l2_val,
        L3: l3_val,
        L4: l4_val
    }

    try:
        θ1a = float(theta1_a.evalf(subs=subs))
        θ1b = float(theta1_b.evalf(subs=subs))
        θ2a = float(theta2_a.evalf(subs=subs))
        θ2b = float(theta2_b.evalf(subs=subs))
    except Exception as e:
        return [f"發生錯誤：{e}"]
        
    def normalize(a):
        return round(a % 360, 4)


    # 組合所有可能構型角度
    results = [
        (normalize(θ1a), normalize(θ2a)),
        (normalize(θ1a), normalize(θ2b)),
        (normalize(θ1b), normalize(θ2a)),
        (normalize(θ1b), normalize(θ2b)),
    ]

    return results
    
print(inverse(-12.77, -117.63, 67.27, 110, 110, 67.27))

Homework << Previous Next >> Plotter